LeetCode-Java题解

WangY. 2020-01-31

目前正在准备实习面试，在LeetCode上刷相关题目。

此博客用于记录一些较难、经典的题目和一些巧妙的解法。

题目及部分代码来自力扣，不断更新中……

1 丑数

1.1 题目介绍

编写一个程序，找出第 n 个丑数。

丑数就是只包含质因数 2, 3, 5 的正整数。

示例:

输入: n = 10

输出: 12

解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

说明:

1 是丑数。
n 不超过1690。

1.2 代码实现

/**
 * 丑数求解过程：首先除2，直到不能整除为止，然后除5到不能整除为止，然后除3直到不能整除为止。
 * 最终判断剩余的数字是否为1，如果是1则为丑数，否则不是丑数
 * 
 * 解题思路：
 * 从1开始遍历，按丑数求解过程找出满足条件的第n个丑数（提交超时）
 * 思路优化（如何利用之前的计算）
 * 解题二：动态规划+三指针
 * dp保存按序排列的丑数，三指针分别是*2，*3，*5，找出下一个丑数
 *
 * @param n
 * @return
 */
public int nthUglyNumber(int n) {
    int[] dp = new int[n];
    dp[0] = 1;
    int i2 = 0, i3 = 0, i5 = 0;
    for (int i = 1; i < n; i++) {
        int min = Math.min(dp[i2] * 2, Math.min(dp[i3] * 3, dp[i5] * 5));
        if (min == dp[i2] * 2) i2++;
        if (min == dp[i3] * 3) i3++;
        if (min == dp[i5] * 5) i5++;
        dp[i] = min;
    }

    return dp[n - 1];
}

1.3 笔记

三指针法。一部分是丑数数组，另一部分是权重2，3，5。下一个丑数，定义为丑数数组中的数乘以权重，所得的最小值。

那么，2该乘以谁？3该乘以谁？5该乘以谁？

其一，使用三个指针idx[3]，告诉它们。比如，2应该乘以ugly[idx[0]]，即数组中的第idx[0]个值。（权重2，3，5分别对应指针，idx[0],idx[1],idx[2]）

其二，当命中下一个丑数时，说明该指针指向的丑数乘以对应权重所得积最小。此时，指针应该指向下一个丑数。（idx[]中保存的是丑数数组下标）

其三，要使用三个并列的if让指针指向一个更大的数，不能用if-else。因为有这种情况：

丑数6，可能由于丑数2乘以权重3产生；也可能由于丑数3乘以权重2产生。
丑数10，… 等等。

2 二叉树的遍历

2.1 前序遍历

2.1.1 前序遍历题目介绍

给定一个二叉树，返回它的前序遍历。

（前序遍历：先访问根节点——左子树——右子树。）

示例:

输入: [1,null,2,3]

1

\

2

/

3

输出: [1,2,3]

2.1.2 前序遍历代码实现

迭代法：

从根节点开始，每次迭代弹出当前栈顶元素，并将其孩子节点压入栈中，先压右孩子再压左孩子。

在这个算法中，输出到最终结果的顺序按照 Top->Bottom 和 Left->Right，符合前序遍历的顺序。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
  public List<Integer> preorderTraversal(TreeNode root) {
    LinkedList<TreeNode> stack = new LinkedList<>();
    LinkedList<Integer> output = new LinkedList<>();
    if (root == null) {
      return output;
    }

    stack.add(root);
    while (!stack.isEmpty()) {
      //检索并弹出栈顶元素
      TreeNode node = stack.pollLast(); 
      //将弹出的元素加入output中
      output.add(node.val);
      
      if (node.right != null) {
        stack.add(node.right);
      }
      if (node.left != null) {
        stack.add(node.left);
      }
        
    }
    return output;
  }
}

算法复杂度：

时间复杂度：访问每个节点恰好一次，时间复杂度为O(N)，其中N是节点的个数，也就是树的大小。
空间复杂度：取决于树的结构，最坏情况存储整棵树，因此空间复杂度是O(N)。

2.2 中序遍历

2.2.1 中序遍历题目介绍

给定一个二叉树，返回它的中序遍历。

（中序遍历：先访问左子树——根节点——右子树。）

示例:

输入: [1,null,2,3]

1

\

2

/

3

输出: [1,3,2]

2.2.2 中序遍历代码实现

解法一：递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List <Integer> inorderTraversal(TreeNode root) {
        List <Integer> res = new ArrayList <> ();
        helper(root, res);
        return res;
    }

	public void helper(TreeNode root, List <Integer> res) {
    	if (root != null) {
       	   if (root.left != null) {
           	  helper(root.left, res);
       	   }
           res.add(root.val);
           if (root.right != null) {
              helper(root.right, res);
           }
        }
    }
}

算法复杂度：

时间复杂度：O(n)。递归函数 T(n) = 2 · T(n/2)+1。
空间复杂度：最坏情况下需要空间O(n)，平均情况为O(logn)。

解法二：基于栈的中序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public List <Integer> inorderTraversal(TreeNode root) {
        List <Integer> res = new ArrayList <> ();
        Stack <TreeNode> stack = new Stack <> ();
        TreeNode curr = root;
        while (curr != null || !stack.isEmpty()) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            res.add(curr.val);
            curr = curr.right;
        }
        return res;
    }
}

算法复杂度：

时间复杂度：O(n)。
空间复杂度：O(n)。

2.3 层次遍历

2.3.1 层次遍历题目介绍

给定一个二叉树，返回其按层次遍历的节点值。

（即逐层地，从左到右访问所有节点）。

示例:

给定二叉树: [3,9,20,null,null,15,7]：

3

/ \

9 20

/ \

15 7

返回其层次遍历结果：[ [3], [9,20], [15,7] ]

2.3.2 层次遍历代码实现

解法一：递归

首先确认树非空，然后调用递归函数 helper(node, level)，参数是当前节点和节点的层次。

程序过程如下：

输出列表称为 levels，当前最高层数就是列表的长度 len(levels)。比较访问节点所在的层次 level 和当前最高层次 len(levels) 的大小，如果前者更大就向 levels 添加一个空列表。
将当前节点插入到对应层的列表 levels[level] 中。
递归非空的孩子节点：helper(node.left / node.right, level + 1)。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    List<List<Integer>> levels = new ArrayList<List<Integer>>();

    public void helper(TreeNode node, int level) {
         // start the current level
         if (levels.size() == level)
             levels.add(new ArrayList<Integer>());
    
         // fulfil the current level
         levels.get(level).add(node.val);
    
         // process child nodes for the next level
         if (node.left != null)
            helper(node.left, level + 1);
         if (node.right != null)
            helper(node.right, level + 1);
    }
    
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root == null) return levels;
        helper(root, 0);
        return levels;
    }
}

算法复杂度：

时间复杂度：O(N)，因为每个节点恰好会被运算一次。
空间复杂度：O(N)，保存输出结果的数组包含 N 个节点的值。

解法二：利用队列实现二叉树的层次遍历

BFS经典实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public List<List<Integer>> levelOrder(TreeNode root) {
    if(root == null)
        return new ArrayList<>();
    
    List<List<Integer>> res = new ArrayList<>();
    Queue<TreeNode> queue = new LinkedList<TreeNode>();
    queue.add(root);
    
    while(!queue.isEmpty()){
        int count = queue.size();
        List<Integer> list = new ArrayList<Integer>();
        while(count > 0){
            //从队首获取元素，同时获取的这个元素将从原队列删除
            TreeNode node = queue.poll();
            list.add(node.val);
            
            if(node.left != null)
                queue.add(node.left);
            if(node.right != null)
                queue.add(node.right);
            count--;
        }
        res.add(list);
    }
    return res;
}

2.4 笔记

如何遍历一棵树

有两种通用的遍历树的策略：

深度优先搜索（DFS）

在这个策略中，我们采用深度作为优先级，以便从跟开始一直到达某个确定的叶子，然后再返回根到达另一个分支。

深度优先搜索策略又可以根据根节点、左孩子和右孩子的相对顺序被细分为先序遍历，中序遍历和后序遍历。
宽度优先搜索（BFS）

我们按照高度顺序一层一层的访问整棵树，高层次的节点将会比低层次的节点先被访问到。

2.5 使用DFS思想解78. 子集

2.5.1 题目介绍

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]

输出:

[

[3],

[1],

[2],

[1,2,3],

[1,3],

[2,3],

[1,2],

[]

]

2.5.2 代码实现

集合中每个元素的选和不选，构成了一个满二叉状态树，比如，左子树是不选，右子树是选，从根节点、到叶子节点的所有路径，构成了所有子集。可以有前序、中序、后序的不同写法，结果的顺序不一样。本质上，其实是比较完整的中序遍历。

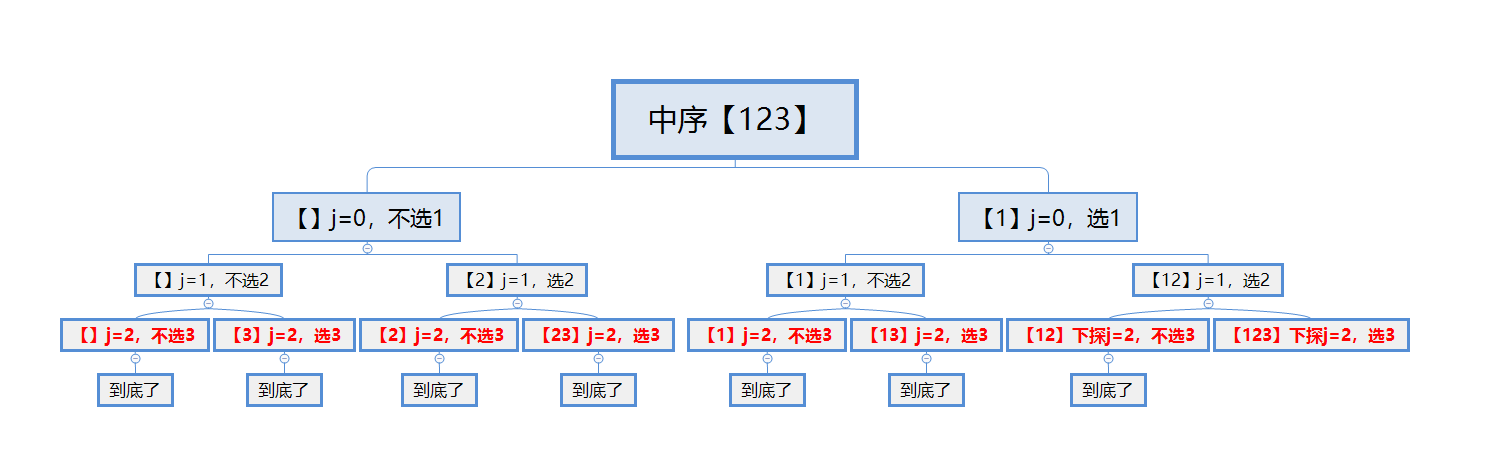
幂集：中序遍历.png

/**
     * DFS，前序遍历
     */
    public static void preOrder(int[] nums, int i, ArrayList<Integer> subset, List<List<Integer>> res) {
        if (i >= nums.length) return;
        // 到了新的状态，记录新的路径，要重新拷贝一份
        subset = new ArrayList<Integer>(subset);

        // 这里
        res.add(subset);
        preOrder(nums, i + 1, subset, res);
        subset.add(nums[i]);
        preOrder(nums, i + 1, subset, res);
    }
    
    /**
     * DFS，中序遍历
     */
    public static void inOrder(int[] nums, int i, ArrayList<Integer> subset, List<List<Integer>> res) {
        if (i >= nums.length) return;
        subset = new ArrayList<Integer>(subset);
    
        inOrder(nums, i + 1, subset, res);
        subset.add(nums[i]);
        // 这里
        res.add(subset);
        inOrder(nums, i + 1, subset, res);
    }
    
    /**
     * DFS，后序遍历
     */
    public static void postOrder(int[] nums, int i, ArrayList<Integer> subset, List<List<Integer>> res) {
        if (i >= nums.length) return;
        subset = new ArrayList<Integer>(subset);
    
        postOrder(nums, i + 1, subset, res);
        subset.add(nums[i]);
        postOrder(nums, i + 1, subset, res);
        // 这里
        res.add(subset);
    }

也可以左子树是选，右子树是不选，相当于，也可以前序、中序、后序的不同写法。程序实现上，需要用一个栈，元素入栈遍历左子树，（最近入栈的那个）元素出栈，遍历右子树。

public static void newPreOrder(int[] nums, int i, LinkedList<Integer> stack, List<List<Integer>> res) {
    if (i >= nums.length) return;
    stack.push(nums[i]);
    // 这里
    res.add(new ArrayList<Integer>(stack));
    newPreOrder(nums, i + 1, stack, res);
    stack.pop();
    newPreOrder(nums, i + 1, stack, res);
}